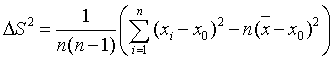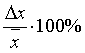Погрешность вычислительного эксперимента.

Для оценки погрешности используют различные числовые характеристики:

Пусть x₁, х₂, ... х_nобозначают n результатов измерений величины, истинное значение которой X:

1. Среднее значение

Среднее значение величины находится по формуле:

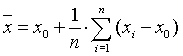
Это среднее значение принимают за приближенное (наиболее вероятное) значение измеряемой величины.

2. Дисперсия

Дисперсия –  среднеквадратичная погрешность. Рассеяние результатов измерений относительно среднего значения принято характеризовать дисперсией ΔS²:

3. Стандартное отклонение

4. Абсолютная погрешность

Абсолютная погрешность результата – доверительный интервал  – Δх – характеризует попадание случайной величины в доверительный интервал  с доверительной вероятностью α:

,

где t_α – коэффициент Стьюдента зависит от доверительной вероятности и числа проведенных экспериментов. В математической статистике коэффициент Стьюдента вычислен для различных значений, и его можно найти в таблице:

Таблица коэффициентов Стьюдента.

n	α
	0.80	0.90	0.95	0.98	0.99	0.995	0.998	0.999
1	3.0770	6.3130	12.7060	31.820	63.656	127.656	318.306	636.619
2	1.8850	2.9200	4.3020	6.964	9.924	14.089	22.327	31.599
3	1.6377	2.35340	3.182	4.540	5.840	7.458	10.214	12.924
4	1.5332	2.13180	2.776	3.746	4.604	5.597	7.173	8.610
5	1.4759	2.01500	2.570	3.649	4.0321	4.773	5.893	6.863
6	1.4390	1.943	2.4460	3.1420	3.7070	4.316	5.2070	5.958
7	1.4149	1.8946	2.3646	2.998	3.4995	4.2293	4.785	5.4079
8	1.3968	1.8596	2.3060	2.8965	3.3554	3.832	4.5008	5.0413
9	1.3830	1.8331	2.2622	2.8214	3.2498	3.6897	4.2968	4.780
10	1.3720	1.8125	2.2281	2.7638	3.1693	3.5814	4.1437	4.5869

Для n = 5 (число измерений) и α = 0.95, коэффициент Стьюдента - 2.570

Обычно для расчетов доверительного интервала пользуются значениями a=0,95; иногда достаточно a=0,90, но при ответственных измерениях требуется более высокая надежность (a = 0,99).

5. Относительная погрешность

Относительная погрешность:

назад