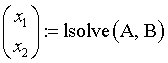Метод наименьших квадратов
Линейная регрессия

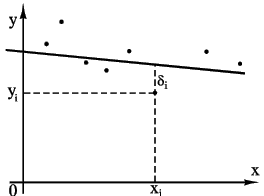Пусть из опыта получены точки (x₁, y₁),(x₂, y₂)(x₃, y₃) ... (x_n, y_n). Требуется найти уравнение прямой  y = ax + b, наилучшим образом согласующейся с опытными точками.

Пусть мы нашли такую прямую. Обозначим через расстояние от опытной i-точки до этой прямой (измеренное параллельно оси y). Очевидно

(1)

Чем меньше числа по абсолютной величине, тем лучше подобрана прямая y=ax+b. В качестве характеристики точности подбора прямой можно принять сумму квадратов

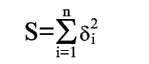(2)

Покажем, как можно подобрать прямую так, чтобы сумма квадратов S была минимальной. Из уравнений (1) и (2) получаем

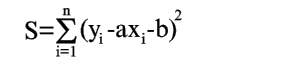(3)

Условия минимума S будут

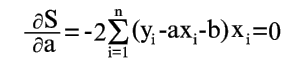(4)

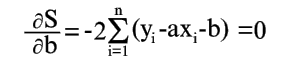(5)

Уравнения (4) и (5) можно записать в виде:

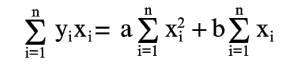(6)

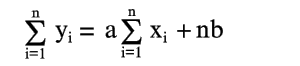(7)

Из уравнений (6) и (7) легко найти a и b по опытным значениям x_i и y_i. Прямая, определяемая уравнениями (6) и (7), называется прямой, полученной по методу наименьших квадратов (этим названием подчеркивается то, что сумма квадратов S имеет минимум). Уравнения (6) и (7), из которых определяется прямая, называются нормальными уравнениями.

Приложение

Решение системы линейных уравнений:

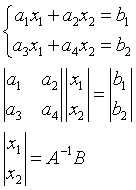
где А^-1 - обратная матрица

В MathCad есть функция решения системы линейных уравнений lsolve(,)

назад