Вариационные ряды и их характеристики

1. Вариационный ряд.

Результаты измерений, опытов и т.д (в математической статистике здесь употребляют слово выборка ) являются труднообозримым набором данных. Для дальнейшего изучения выборку подвергают перегруппировке.

По этому ряду уже можно сделать несколько выводов. Например, средний элемент вариационного ряда (медиана) может быть оценкой наиболее вероятного результата измерения. Первый и последний элемент вариационного ряда (т.е. минимальный и максимальный элемент выборки) показывают разброс элементов выборки. Иногда если первый или последний элемент сильно отличаются от остальных элементов выборки, то их исключают из результатов измерений, считая, что эти значения получены в результате какого-то грубого сбоя, например, техники.

2. Группировочный статистический ряд.

Этот ряд даёт представление о том, как распределены результаты измерений между максимальным и минимальным значением. Для того  чтобы дать строгое определение группированного статистического ряда, рассмотрим его построение.

Пусть N – число элементов выборки, x₀– минимальный элемент выборки, x_N – максимальный элемент выборки. Разобьем отрезок [x₀, x_N ] на n равных частей, где

n =1+3.31 lg N  (формула Старджесса)

Таким образом, получим набор непересекающихся промежутков

Δ₁ = [x₀, x₁),  Δ₂ = [x₁, x₂), …, Δ_{n -1} = [ x_{n -2}, x_{n - 1}), Δ_n = [ x_{n - 1}, x_N]

Длина каждого промежутка (шаг) Δ_k = [ x_k-1, x_k ), где k = 1, 2, …, n,  вычисляется по формуле   

Найдём число элементов выборки, попадающих в каждый из промежутков. Пусть m_k – число элементов выборки, попавших в промежуток Δ_k. Это число также называют абсолютной частотой попадания в промежуток Δ_k.

Группировочный статистический ряд характеризуется также:

относительной частотой – отношение числа элементов выборки, попавших в промежуток Δ_k к общему числу элементов, т.е. m_k / N

Совокупность промежутков и соответствующих им частот (абсолютных и относительных) называют группированным статистическим рядом. Обычно сами промежутки заменяют их серединами, которые вычисляются по формуле 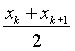, а в качестве частот берут приведённые частоты.

Графическое представление группированного статистического ряда.

Существует несколько способов графического изображения рядов (гистограмма, полигон, кумулята), выбор которых зависит от цели исследования и от вида вариационного ряда.

Гистограмма служит только для представления интервальных вариационных рядов и имеет вид ступенчатой фигуры из прямоугольников с основаниями, равными длине интервалов Δ, и высотами, равными m_k абсолютным частотам.

Полигон представляет собой ломаную, соединяющую точки плоскости с координатами: первая - середина промежутка, вторая – абсолютным частотам m_k или относительная частота m_k / N

Эмпирическая функция распределения

Полигон частот иногда называют эмпирической функцией плотности вероятности, а функцию плотности, которая в действительности соответствует нашему процессу и которую мы оцениваем f(x) – генеральной функцией плотности вероятности.

Смысл этой функции заключён в следующем (см. рис.1.): площадь фигуры, ограниченной графиком функции плотности вероятности f(x), снизу осью абсцисс Ох, слева – прямой x=a, справа прямой x=b равна вероятности P того, что измеряемая величина, значения которой мы получаем в ходе эксперимента, примет значения от a до b:

Функцию F(x) называется генеральной функцией распределения, а кривая, ее оценивающая и получающаяся из выборки, называется эмпирической функцией распределения.

Для построения эмпирической функции распределения нужно вычислить накопленные частоты для каждого промежутка группированного статистического ряда w_x:

Пусть х некоторое число. Тогда количество вариант m_k значения которых меньше х, называется накопленной частотой, т.е.

Для первого промежутка эта частота равна 0, для для второго - относительной частоте попадания в первый промежуток, для третьего– сумме относительных частот попадания в первый и второй промежутки, для четвертый – сумме относительных частот попадания в первый, второй и третий промежутки и т.д.

Кумулянта есть графическое изображение вариационного ряда, когда на вертикальной оси откладываются накопленные частоты или частности, а на горизонтальной - значения признака или середину промежутка.

Отношение накопленной частоты к общему числу наблюдений N называется относительной накопленной частотой или накопленной частостью w_k / N.

Ломанная, соединяющая точки, первая координата которых – середина промежутка, а вторая равна относительной накопленной частоте и будет эмпирической функцией распределения.

Ссылки:

1. Вариацинные ряды и их характеристики

назад