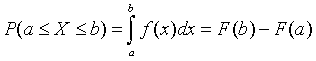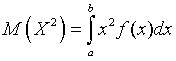|
Календарный план Самостоятельная работа студентов |
Функция распределения. Числовные характеристики непрерывной случайной величины.
Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений. Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
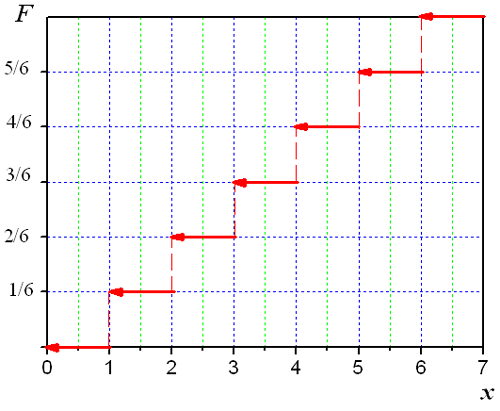
Если X - случайная величина, то функция F(x) - интегральная функция распределения вероятностей, или просто функция распределения (иногда применяют термин кумулятивная функция распределения) случайной величины определяет вероятность P того, что случайная величина принимает значение, меньше x, т.е.
F(x) = P( X < x)
Функция распределения содержит всю информацию о случайной величине, поэтому изучение случайной величины заключается в исследовании ее функции распределения.
Функция распределения полностью характеризует случайную величину и является одной из форм закона распределения.
Из определения следует, что функция распределения любой случайной величины обладает следующими свойствами:
Свойства F(x):
1. Интегральная функция распределения принимает значения от 0 до 1.
2. F(x) - неубывающая функция, то есть F(x2)
F(x1), если x2 > x1.
3. Вероятность того, что случайная величины X примет значение, заключенное в интервале (а, b) равна приращению интегральной функции распределения на этом интервале:
4. Если все значения непрерывной случайной величины принадлежат некоторому промежутку от a до b, то:
F(x) = 0, если x
a,
F(x) = 1, если xb
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Например для функции распределения числа очков выпавших при одно бросании игральной кости.
Непрерывную случайную величину удобнее характеризовать плотностью распределения (дифференциальной функцией распределения)
:
![]()
Следовательно, функция распределения F(x) выражается через плотность распределения:
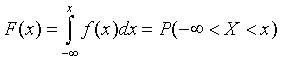
|
График
называют также законом распределения или кривой распределения.
Свойства ![]() :
:
1.
0
2.
, если все возможные значения X принадлежат интервалу (a, b)
Числовые характеристики непрерывных случайных величин
Если все значения непрерывной случайной величины принадлежат некоторому промежутку от a до b, то математическое ожидание непрерывной случайной величины X:
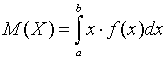
Матаматическое ожидание - определяет среднее значение случайной величины Х
Дисперсия - отклонение случайной величины Х от среднего значения
,
где
Cреднеквадратическое отклонение
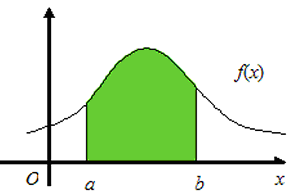 Вероятность того, что непрерывная случайная величина X примет значение, принадлежащие интервалу (a, b) равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащие интервалу (a, b) равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b: