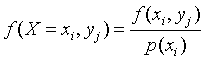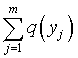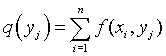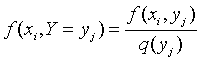Двумерные случайные величины

Двумерная случайная величина задается в виде интегральной функции:

F(x, у) = Р(Х < х, Y < y),

которая означает вероятность того, что случайная величина примет значения меньше Х и меньше Y одновременно.

Закон распределения дискретной двумерной случайной величины можно представить в виде таблицы, где ƒ(x_i, y_j) совместная плотность распределения двумерной случайной величины :

xi \ yj	y1	y2	…	ym
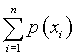
x1	ƒ(x1, y1)	ƒ(x1, y2)	…	ƒ(x1, ym)	p(x1)
x2	ƒ(x2, y1)	ƒ(x2, y2)	…	ƒ(x2, ym)	p(x2)
…	…	…	…	…	…
xn	ƒ(xn, y1)	ƒ(xn, y2)	…	ƒ(xn, ym)	p(xn)
	q(y1)	q(y2)	…	q(ym)	1

Если случайные величины х и у независимы, то

ƒ(x, y) = p(x) q(y),

где p(x) - безусловная плотность распределения случайной величины x, q(y) - безусловная плотность распределения случайной величины y.

,

Условным распределением случайной величины x при заданном значении Y = y_j называют

Условным распределением случайной величины y при заданном значении X = x_i называют

Числовые характеристики системы двумерных случайных величин