|
Самостоятельная работа студентов |
| << Предыдущая | Оглавление | Следующая >> |
3. Алгоритм и его свойства .
Алгоpитм — заранее заданное понятное и точное предписание возможному исполнителю совершить определенную последовательность действий для получения решения задачи за конечное число шагов.
Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая, биологическая или биотехническая) система, способная выполнить действия, предписываемые алгоритмом.
Исполнителя хаpактеpизуют:
- среда;
- элементарные действия;
- система команд;
- отказы.
Среда (или обстановка) — это "место обитания" исполнителя.
Система команд . Каждый исполнитель может выполнять команды только из некоторого строго заданного списка — системы команд исполнителя. Для каждой команды должны быть заданы условия применимости (в каких состояниях среды может быть выполнена команда) и описаны результаты выполнения команды . После вызова команды исполнитель совершает соответствующее элементарное действие .
Отказы исполнителя возникают, если команда вызывается при недопустимом для нее состоянии среды.
Основные свойства алгоритмов :
1. Понятность для исполнителя — исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.
2. Дискретность (прерывность, раздельность) — алгоpитм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов (этапов).
3. Определенность — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический хаpактеp и не требует никаких дополнительных указаний или сведений о решаемой задаче.
4. Результативность (или конечность) состоит в том, что за конечное число шагов алгоpитм либо должен приводить к решению задачи, либо после конечного числа шагов останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение времени, отведенного для исполнения алгоритма, с выдачей промежуточных результатов.
5. Массовость означает, что алгоpитм решения задачи pазpабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Виды алгоритмов
Алгоритмы как логико-математические средства отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы, в зависимости от цели, начальных условий задачи, Петей ее решения, определения действий исполнителя подразделяются следующим образом:
• механические алгоритмы (детерминированные, жесткие, например, алгоритм работы машины, двигателя). Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм;
• гибкие алгоритмы:
• вероятностные (стохастические) алгоритмы дают программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата;
• эвристические алгоритмы – это алгоритмы, в которых достижение конечного результата программы действий однозначно не определено, так же как не обозначена вся последовательность действий исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.
• линейные алгоритмы – наборы команд (указаний), выполняемых последовательно во времени друг за другом;
• разветвляющиеся алгоритмы – алгоритмы, содержащие хотя бы одно условие, в результате проверки которого компьютер обеспечивает переход на один из двух возможных шагов;
• циклические алгоритмы – алгоритмы, предусматривающие многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов;
• вспомогательные (подчиненные) алгоритмы (процедуры) – алгоритмы, ранее разработанные и целиком используемые при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи так же выделяют вспомогательные алгоритмы.
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов .
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.
Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
1. Базовая структура "следование". Образуется последовательностью действий, следующих одно за другим:
Школьный алгоритмический язык |
Язык блок-схем |
действие 1 |
|
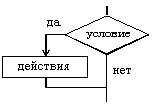
2. Базовая структура "ветвление" . Обеспечивает в зависимости от результата проверки условия ( да или нет ) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу , так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Структура ветвление существует в четырех основных вариантах:
- если—то;
- если—то—иначе;
- выбор;
- выбор—иначе.
Школьный алгоритмический язык |
Язык блок-схем |
1. если—то |
|
| если условие то действия все |
|
2. если—то—иначе |
|
| если условие то действия 1 иначе действия 2 все |
|
3. выбор |
|
| выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N все |
|
4. выбор—иначе |
|
| выбор при условие 1: действия 1 при условие 2: действия 2 . . . . . . . . . . . . при условие N: действия N иначе действия N+1 все |
|
Примеры структуры ветвление
Школьный алгоритмический язык |
Язык блок-схем |
| если x > 0 то y := sin(x) все |
|
| если a > b то a := 2*a; b := 1 иначе b := 2*b все |
|
| выбор при n = 1: y := sin(x) при n = 2: y := cos(x) при n = 3: y := 0 все |
|
| выбор при a > 5: i := i+1 при a = 0: j := j+1 иначе i := 10; j:=0 все |
|
3. Базовая структура "цикл". Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла . Основные разновидности циклов представлены в таблице:
Школьный алгоритмический язык |
Язык блок-схем |
Цикл типа пока . |
|
| нц пока условие тело цикла (последовательность действий) кц |
|
Цикл типа для . |
|
| нц для i от i1 до i2 тело цикла (последовательность действий) кц |
|
Примеры структуры цикл
Школьный алгоритмический язык |
Язык блок-схем |
| нц пока i <= 5 S := S+A[i] i := i+1 кц |
|
| нц для i от 1 до 5 X[i] := i*i*i Y[i] := X[i]/2 кц |
Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока . Выход из итерационного цикла осуществляется в случае выполнения заданного условия.
На каждом шаге вычислений происходит последовательное приближение к искомому результату и проверка условия достижения последнего.
Пример. Составить алгоритм вычисления бесконечной суммы

с заданной точностью ![]() (для
данной знакочередующейся бесконечной суммы требуемая точность будет достигнута,
когда очередное слагаемое станет по абсолютной величине меньше
(для
данной знакочередующейся бесконечной суммы требуемая точность будет достигнута,
когда очередное слагаемое станет по абсолютной величине меньше ![]() ).
).
Алгоритм на школьном АЯ |
Блок-схема алгоритма |
| алг Сумма ( арг вещ x, Eps, рез вещ S) дано | 0 < x < 1 надо | S = x - x**2/2 + x**3/3 - ... нач цел i, вещ m, p ввод x, Eps S := 0; i := 1 | начальные значения m := 1; p := -1 нц пока abs(m) > Eps p := -p*x | p - числитель | очередного слагаемого m := p/i | m - очередное слагаемое S := S + m | S - частичная сумма i := i + 1 | i - номер | очередного слагаемого кц вывод S кон |
|
Пример вложенных циклов для
Вычислить сумму элементов заданной матрицы А(5,3).
Матрица
А |
|
S := 0; нц для i от 1 до 5 нц для j от 1 до 3 S:=S+A[i,j] кц кц |
Пример вложенных циклов пока
Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.
|
i:=2; P:=1 нц пока i <= 10 j:=2 нц пока j <= 10 P:=P*A[i,j] j:=j+2 кц i:=i+2 кц |
Алгоритм, в состав которого входит итерационный цикл, называется итеpационным алгоpитмом. Итерационные алгоритмы используются при реализации итерационных численных методов.
В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла ( сходимость итерационного процесса ). В противном случае произойдет "зацикливание" алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность .
| << Предыдущая | Оглавление | Следующая >> |